Table of Contents
When objects are submerged in water, they appear bent. This is due to the science of refraction. Refraction is the process at which wave propagation changes as the medium of transmission also changes. The phenomenon is dependent on the conservation of both energy and momentum. As the medium changes, there is also a change in the phase velocity of the wave, but the frequency remains unchanged. This action mostly takes place when waves pass from one medium to the other at any angle greater than 00 relative to the normal. Refraction is described by Snell’s, law which states that “the ratio of the sines of the angle of incidence and that of refraction is equivalent to the ration of the phase velocities in the two media or equal to the reciprocal of the ratio of the indices of refraction” (Nave, 2010).
There are many different ways in which the behavior of light is seen, and one of the specific properties of light is that it is possible to alter its velocity in consideration to the medium that it passes through. As light enters the new medium, which is water in this case, its velocity is slowed down, thereby bending it to another new angle, different from where it was viewed initially. This bending effect is refractive to the very position of the object. The principle of refraction has its mathematical explanation through Snell’s law stated above, which was discovered around 1621 by a scientist known as Willebrord Snell. The expression of Snell’s law is as follows
sin θ1 sin θ2 =v1v2=n2n1
In the expression above, θ1 is the angle of incidence, while θ2 is the angle of refraction. The angle of incidence is the angle which measures the approach that the ray of light makes at the surface, which is the water surface in this case. The angle of refraction on the other hand, is the angle that is made in the new medium as a result of bending of the light.
Snell’s law is utilized in the determination of the direction which light rays take through a refractive media having varying indices of refraction. Such refractive indices are labeled n1, n2, and n3 and so on, representing the factor by which the speed of light rays decreases when traveling through a medium of refraction, such as water or glass as opposed to its velocity within the medium. When light passes at the border of the media, the light will be refracted to either a smaller or a greater angle depending on the relative indices of the two media. All the angles are measured in relation to the normal line, which is represented by a perpendicular boundary. When light travels from air to water, the refraction of light would be towards the normal line since the speed of light is slowed down when in water. On the other hand, light traveling from water to air would give refraction away from the normal line. Refraction taking place between two surfaces is a reversible one since the angles would be the same for light traveling in the opposite direction if all conditions were similar. Snell’s law generally applies only for specular or isotropic media like glass. In anisotropic media like crystals, the refracted ray may be split by birefringence into two rays, the ordinary o-ray which obeys Snell’s law and the extraordinary e-ray which is not co-planar with the incident ray (Weisstein, 2010).

The aim of this experiment was to find out how the increase in sugar concentration in water has an effect in the angle of refraction in water. The experiment thus involved the variation of sugar concentration in order to observe the effect it has on the angle of refraction in water, that is, where it lowers or increases the angle of refraction.
Hypothesis
An increase in the molarity of sugar water by a constant amount of 0.2M leads to a corresponding linear increase in the calculated index of refraction. Thus in this experiment, the hypothesis was that any increase in sugar concentration will lead to a corresponding increase in the angle of refraction. This is on the basis of Snell’s law. To prove this, the angle of refraction was measured in comparison with the amount of sugar existing in the water so as to find out the effect it has on the angle of refraction. This hypothesis thus to be proved through the experiment, but its basis originated from the fact that there is a uniform increase and decrease in the angle of refraction on the basis of the density of the medium through which light passes. In this experiment, the variables were as follows: the independent variable was the molarity of sugar water, while the dependent variable was the refractive index for the sugar water. On the other hand, the controls considered in the experiment were angle of incidence and the horizontal distance of the laser from the wall.
Experimental Apparatus
- Stirring rod
- 1260 grams of sugar
- Flour
- Water
- Laser
- Clamping feed neck
- Square beaker
- Ruler
- Protractor
- Clamp stand
- Balance
- Various beakers
1 mole of sugar =180 g
Chemical formula for sucrose C12H22O11
Sucrose solubility in 100 ml water =67.89. This gives a total of 407.34 for 600 ml.
Experimental Procedure
The laser was placed perpendicular to the wall and in front of it, followed by a clear square beaker whose base was placed parallel to the wall ground and the other parts of its body placed parallel to the wall. The beaker was first filled using plain water. The distance from the point at which the prism was excited by the laser and the wall was then measured and marked as the horizontal distance. Again, the distance from the point that the laser struck the wall to the point where the horizontal struck the wall was also measured and marked as the vertical distance. The next steps and further trials in the experiment involved the use of sugar water whose molarity was 0.2 M. The setup was as shown below (fig. 1).

Figure 1. Setting of the experiment
Calculations
The refraction of the laser was seen to take place, that is, when entering the beaker and when leaving it. In this case, a simple Snell’s law did not suffice in the experiment, thus prompting the derivation of a combination of equations to match the situation using the relationship of angles: Considering the angle of incidence to be 10, shift to the right at 0 mol, that is, when 0 grams of sugar is added, and 0.80 shift to the left at 1/3 mol when 60g of sugar is added, Snell’s law applies as follows
1xsin300=n2sin0.8
θ2=60-θ3
n2sinθ3=1xsinθ4 (Snell‘s law)
Using the equations above, it is possible to derive an equation defining the relationship betweenθ4, which is the angle to be calculated, and n2, which is the refractive index of the sugar water. The equation is as shown below
n2=12sin (60-sinθ4n2
From the vertical and the horizontal distances measured, θ4 was calculated from
θ4=vertical distancehorizontal distance +300
Results
The results obtained were as shown in table 1 below
| Concentration | trials | ||
| 0 mol (0g) | shift 1 degree right | ||
| 1/3 mol (60g) | 0.8 degree left | ||
| 2/3 mol (120g) | 1 degree left | ||
| 1 mol (180g) | 1.3 degree left | ||
| 1 + 1/3 mol (240g) | 1.6 degree left | ||
| 1 + 2/3 mol (300g) | 1.8 degree | ||
| 2 mol (360g) | 2 degrees | ||
This was then used in drawing the graph as shown below (fig.2).
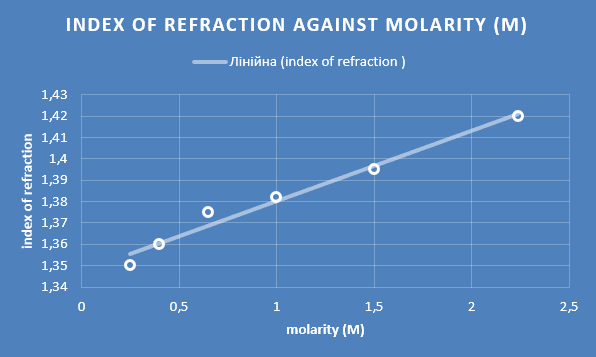
Figure 2. Refraction index
Discussion
When sugar is added to the solution, it is seen to get cloudy. This is partly because there is change in its refractive index and partly due to its particles scattering light that comes through it. When there is complete dissolution of all particles and a uniform solution is obtained, there is change in the refractive index since the sugar molecules polarize the solution in comparison to the water molecules. Starting with the micro-polarization vector p, the expression is given by
p=∝*E
Where represent the polarity of the molecules, p is the micro-polarization vector and E is the electric field applied in the process of polarization. In the presence of the concentration of sugar, the vector for macro-polarization is as follows
P=Np=N∝*E=xE
In this case, N represents the density of sugar molecules and x is the electric susceptibility. Thus the total susceptibility is obtained by adding that of sugar and water. Again, the electric permittivityε=1+x, while the expression for the refractive index in terms of permittivity isεμc. From this relation, the refractive index will increase when sugar is added, since they ate directly proportional to each other. Sugar has a property known as optical rotatory dispersion, meaning that since it is chiral, it will bear different refractive indices on both right and left hand hence the result shown in table 1 has both results for left and right polarization. This causes the polarized light to rotate in polarization while travelling through the sugar solution.
The higher the sugar concentration, the more the light that is caused to bend, that is, a high refractive index; which is seen to increase as the solution gets thicker. This leads to the formation of a denser medium in the liquid, whose refractive index is also high. As the projection distance increases, the resolution of the laser increases, that it, its focus had to be given fine adjustment in order to achieve better results. This experiment is relevant and its conclusions applicable in the industries that involve mass production of soft drinks and other areas involving dissolving liquids with sugar. The light path from the laser acted as the pipes through which the liquid flows in the real life application, and is used to measure the continuous flow of the amount of sugar. In such real world applications in the dissolution industries, there is a signal given when the sugar flow is too little, thus more is added to the solution, and another signal when there is excess sugar, thus the sugar flow is reduced in order to maintain the required amount in the drink or other products.
Conclusion
The results obtained from the calculations were almost perfectly linear, and had a correlation coefficient of 0.9896. This falls in the range of 0 to 1, where 0 represents no correlation and 1 represents a total positive correlation. This value thus demonstrates that there is a strong positive correlation between the measured parameters. There was a nearly uniform increment in the indices of the correlation with a corresponding increase in the molarity of the solution in the beaker. This ultimately confirms that the hypothesis stated herein is true, that there is increase in the index of refraction as the sugar content also increases. As the density of the substance increased, the angle and the refractive index also increased. The increase of the latter two were caused by the increase in the density of the substance. In order to ensure that better accuracy was achieved, the distance between the laser and the beaker was maximized. This thus led to an increase in the dimensions of the vertical and the horizontal distances and a consequent increase in the accuracy of the calculated angle, thus leading to low uncertainty and high correlation coefficient.
The uncertainty which was calculated using brute force method for each index of refraction was obtained to be 0.00020 and 0.00026. The index for 0M was compared to the 1.3330 index for water. Since the calculated index for water was 1.341, the percentage error obtained in this experiment was 0.6%. This error resulted from various sources such as the scale used to measure the quantities of sugar which was imperfect, the difficulties in the logistics for measuring the distance between the laser and the beaker using the ruler, parallax error of the water due to meniscus and the position of the laser to the beaker which was not perfectly perpendicular. This experiment can be improved by using equipment which is more precise in sugar measurement and a better method for finding the distance from the beaker to the laser, together with ensuring that the laser is perfectly perpendicular to the beaker. With this, the percentage error in the experiment can be reduced.
- Nave, R. (2010). Refraction of light. Georgia State University.
- Weisstein, E. (2010). Snell’s law. Wolfram Research.


